
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:35.
- Viimati modifitseeritud 2025-06-01 05:04.
Mõelge lihtsalt 2x2-le maatriks see on sarnane selle pöördväärtusega ilma et diagonaalkirjed oleksid 1 või -1. Diagonaal maatriksid teeb. Niisiis, A ja vastupidine A on sarnased , seega on nende omaväärtused samad. kui üks A omaväärtustest on n, siis omaväärtused selle pöördvõrdeline on 1/n.
Samuti küsiti, kas maatriks sarnaneb selle transponeerimisega?
Mis tahes ruut maatriks üle põllu on sarnane selle ülevõtmisega ja mis tahes ruudu kompleks maatriks on sarnased sümmeetriliseks kompleksiks maatriks.
Samuti, kas kõik pööratavad maatriksid on sarnased? Kui A ja B on sarnased ja ümberpööratav , siis on A-1 ja B-1 sarnased . Tõestus. Alates kõik a maatriksid on ümberpööratav , võime võtta mõlema poole pöördväärtused: B-1 = (P-1AP)-1 = P-1A-1(P-1)-1 = P-1A-1P, seega on A-1 ja B-1 sarnased . Kui A ja B on sarnased , nii on Ak ja Bk iga k = 1, 2,.
Kas maatriks võib sellega seoses olla iseendaga sarnane?
See tähendab, ükskõik milline maatriks on endaga sarnane : I-1AI=A. Kui A on sarnased B-le, siis B on sarnased A-le: kui B=P−1AP, siis A=PBP−1=(P−1)−1BP−1. Kui A on sarnased B-le B=P−1AP kaudu ja C on sarnased B-le C=Q−1BQ kaudu, siis A on sarnased C-sse: C=Q−1P−1APQ=(PQ)−1APQ.
Mida see tähendab, kui maatriksid on sarnased?
Lineaaralgebras kaks n-x-n maatriksid A ja B kutsutakse sarnane, kui on olemas inverteeritav n-by-n maatriks P selline et. Sarnased maatriksid kujutavad sama lineaarset kaarti kahe (võimalik) erineva aluse all, kusjuures P on aluse muutus maatriks.
Soovitan:
Kuidas on sõna maatriks seotud mitokondritega?
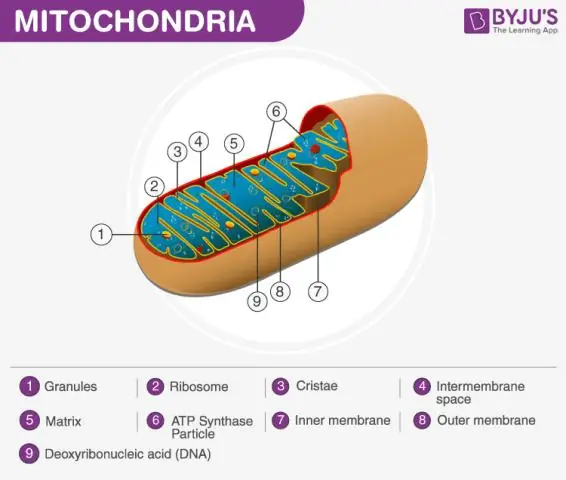
Määratletud mitokondriaalne maatriks Mitokondrid koosneb välismembraanist, sisemembraanist ja geelitaolisest materjalist, mida nimetatakse maatriksiks. See maatriks on viskoossem kui raku tsütoplasma, kuna see sisaldab vähem vett. See on rakuhingamise oluline samm, mis toodab energiamolekule, mida nimetatakse ATP-ks
Mida teeb rakuväline maatriks?

Oma mitmekesise olemuse ja koostise tõttu võib ECM täita paljusid funktsioone, nagu näiteks toe pakkumine, kudede eraldamine üksteisest ja rakkudevahelise suhtluse reguleerimine. Rakuväline maatriks reguleerib raku dünaamilist käitumist
Mis on vere rakuväline maatriks?

Ekstratsellulaarne maatriks, mida nimetatakse plasmaks, muudab vere sidekudede seas ainulaadseks, kuna see on vedel. See vedelik, mis on enamasti vesi, peatab püsivalt moodustunud elemendid ja võimaldab neil kogu kehas kardiovaskulaarsüsteemis ringelda
Kas rõhk on pindalaga pöördvõrdeline?

Rõhk on defineeritud kui jõud pindalaühiku kohta. Rõhk on pindalaga pöördvõrdeline, st pindala suurenedes rõhk suureneb
Kas gaasi maht on otse või pöördvõrdeline?

Antud gaasiproovi maht on otseselt võrdeline selle absoluutse temperatuuriga konstantsel rõhul (Charles'i seadus). Teatud koguse gaasi maht on pöördvõrdeline selle rõhuga, kui temperatuuri hoitakse konstantsena (Boyle'i seadus)
