Video: Kuidas konstrueerida dilatatsiooni skaalateguriga 2?
2024 Autor: Miles Stephen | [email protected]. Viimati modifitseeritud: 2023-12-15 23:35
Suurenduse loomiseks a mastaabitegur ''-st 2 '': tõmmake sirgjooned, mis ühendavad iga tippu keskpunktiga laienemine . Kasutage kompassi, et leida punktid, mis on keskpunktist kaks korda kaugemal laienemine kui algsed tipud. Ühendage uued tipud, et moodustada laienenud pilt.
Samamoodi küsitakse, kuidas laiendada skaalateguri 2 võrra?
Laienemine koos mastaabitegur 2 , korrutage arvuga 2 . Alustades nelinurgast ABCD (sinine), joonistage laienemine pilt nelinurgast, mille keskpunkt on lähtepunktis ja a mastaabitegur ½-st. ABCD iga tipp korrutatakse ½-ga. Laienemine koos mastaabitegur ½, korruta ½-ga.
Lisaks, mis on laienemise reegel? Märkus reegel on järgmises vormis Dk(x, y)=(kx, ky) ja ütleb, et eelkujutis on läbinud a. laienemine päritolu kohta mastaabiteguri k järgi. Kui k on suurem kui üks, siis laienemine pilt on suurem kui. eelpilt. Kui k on vahemikus 0 kuni 1, siis laienemine pilt on väiksem kui eelpilt.
Samamoodi küsitakse, mida tähendab laiendatud skaalateguriga 2?
Näide 1. Alloleval pildil on a laienemine koos mastaabitegur 2 . See tähendab et kujutis A' on kaks korda suurem kui eelkujutis A. Sarnaselt teiste teisendustega kasutatakse kujutise eelkujutisest eristamiseks algtähistust. Pildil on alati pärast tähte, näiteks A', algustäht.
Mis on mastaabitegur 1 2?
Mõelge näiteks kahele sarnasele ruudule. Ühe külje pikkus on 2 tolli ja teise külje pikkus 4 tolli. See annab a mastaabitegur 1:2 väikeselt väljakult suurele väljakule. Nendel kahel sarnasel ruudul on a mastaabitegur 1:2 väikeselt väljakult suurele väljakule.
Soovitan:
Kuidas leida koordinaattasandil dilatatsiooni mõõtkava?
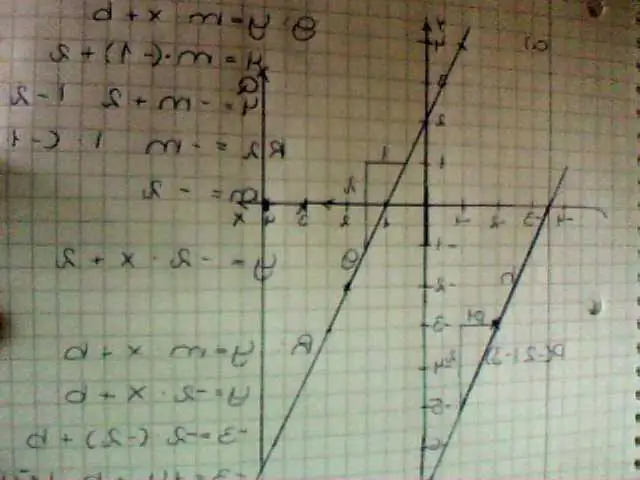
Joonistage kolmnurga ABC graafik koordinaatidega A(2, 6), B(2, 2), C(6, 2). Seejärel laiendage pilti mõõtkava teguriga 1/2, kusjuures laienemise keskpunktiks on alguspunkt. Esiteks joonistame oma algse kolmnurga koordinaattasandil graafiku. Järgmisena korrutame iga koordinaadi mastaabiteguriga 1/2
Kuidas konstrueerida risti asetsev joonelõik?
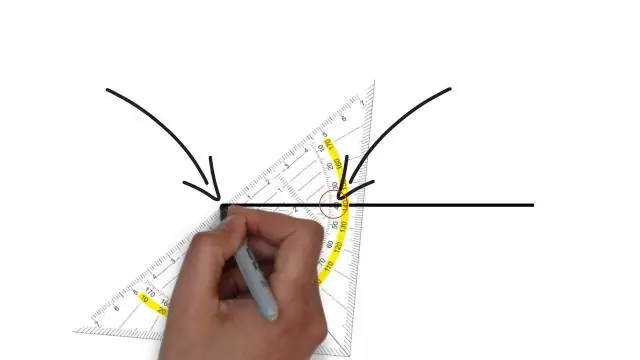
Konstruktsioon: sirge, mis läbib P risti antud joonega. SAMMUD: asetage kompassi punkt asendisse P ja pöörake mis tahes suurusega kaar, mis ületab joone kaks korda. Asetage kompassipunkt ühte kahest kohast, kus telg ületas joone, ja tehke väike kaar joonest allapoole (poolel, kus P ei asu)
Kuidas konstrueerida kompassiga nurga koopiat?
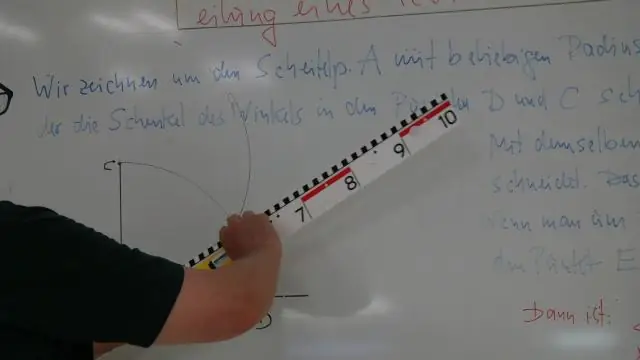
Nurka kopeerimine kompassi abil Joonistage tööjoon l, millel on punkt B. Avage oma kompass suvalise raadiusega r ja konstrueerige nurga A kahte külge punktides Liiva T lõikav nurk (A, r). Ehitage kaar (B, r), mis lõikub sirgega l mingis punktis V. Ehitage kaar (S, ST). Ehitage kaar (V, ST) lõikuva kaar (B, r) punktisW
Kuidas konstrueerida risti?
Konstruktsioon: sirge, mis läbib P risti antud joonega. SAMMUD: asetage kompassi punkt asendisse P ja pöörake mis tahes suurusega kaar, mis ületab joone kaks korda. Asetage kompassi punkt ühte kahest kohast, kus telg ületas joone, ja tehke väike kaar joone alla (poolele, kus P ei asu)
Kuidas konstrueerida geomeetrias koordinaattasapinda?
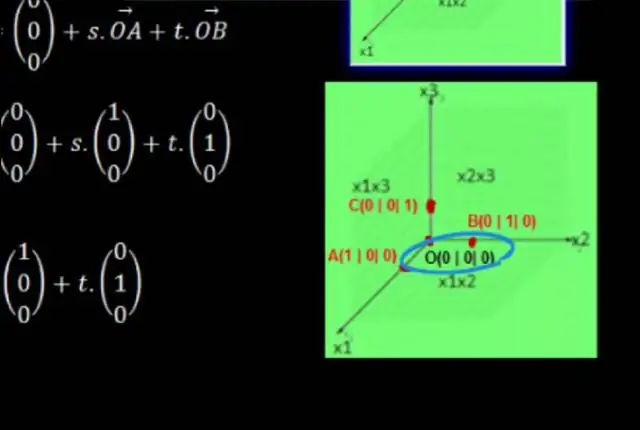
Koordinaattasapinna loomiseks toimime järgmiselt: Joonistage kaks üksteisega risti asetsevat arvjoont, mis ristuvad mõlema sirge punktis 0. Märgistage horisontaalne arvjoon x-teljeks ja vertikaalne arvjoon y-teljeks