
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Viimati modifitseeritud 2025-01-22 16:57.
The avaldus r s on tingimusliku definitsiooni järgi tõene. The avaldus s r on ka tõsi. Seetõttu on lause "Kolmnurk on võrdhaarne siis ja ainult siis, kui sellel on kaks kongruentset (võrdset) külge" kahetingimuslik . Kokkuvõte: A kahetingimuslik väide on defineeritud kui tõene, kui mõlemal osal on sama tõeväärtus.
Veelgi enam, milline on kahetingimustelise avalduse näide?
Kahe tingimusliku avalduse näited The kahetingimuslikud väited nende kahe hulga jaoks oleks: Hulknurgal on ainult neli külge siis ja ainult siis, kui hulknurk on nelinurk. Hulknurk on nelinurk siis ja ainult siis, kui hulknurgal on ainult neli külge.
Lisaks, mis on geomeetrias bikonditsionaal? A kahetingimuslik lause on kombinatsioon tingimuslausest ja selle vastupidisest vormist, mis on kirjutatud siis ja ainult kui kujul. Kaks sirglõiku on kongruentsed siis ja ainult siis, kui nad on võrdse pikkusega. A kahetingimuslik on tõene siis ja ainult siis, kui mõlemad tingimussõnad on tõesed.
Millal saate sellega seoses kirjutada kahetingimustelise avalduse?
' Kahetingimustelised väited on tõesed avaldused mis ühendavad hüpoteesi ja järelduse võtmesõnadega „siis ja ainult siis. ' Näiteks avaldus tahe võta see vorm: (hüpotees) siis ja ainult siis (järeldus). Me võiksime samuti kirjutada see nii: (järeldus) siis ja ainult siis (hüpotees).
Mida IFF kahetingimustelises avalduses tähendab?
Loogikas ja matemaatikas loogiline kahetingimuslik , mida mõnikord nimetatakse materjaliks kahetingimuslik , on loogiline ühend, mida kasutatakse kahe ühendamiseks avaldused ja moodustada avaldus "kui ja ainult siis", kus on tuntud kui eelkäija ja tagajärg. Seda lühendatakse sageli kui " iff ".
Soovitan:
Mis on loogikas bikonditsionaalne väide?

Kui kombineerime kaks tingimuslauset sel viisil, saame kahetingimusliku. Definitsioon: kahetingimusteline väide on defineeritud tõeseks, kui mõlemal osal on sama tõeväärtus. Kahe tingimusega p q tähistab p siis ja ainult siis, kui q, kus p on hüpotees ja q on järeldus
Mis on jagatis matemaatika näites?
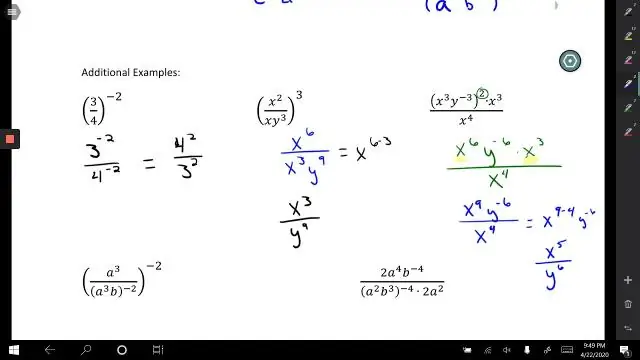
Vastus pärast ühe arvu jagamist teisega. dividend ÷ jagaja = jagatis. Näide: 12 ÷ 3 = 4, 4 on jagatis
Mis on kommensalism bioloogia näites?

Kommensalismi näited. Kommensalism on sümbiootiline suhe, kus üks organism saab kasu ja teist organismi ei aitata ega kahjustata. Näidete hulka kuuluvad hagarlind ja veised, orhideed ja puud, kõrts, takjas umbrohi ja remora
Mis on matemaatika näites Subtrahend?

Arv, mis tuleb lahutada. Teine arv lahutamisel. minuend − alamosa = erinevus. Näide: in 8 &miinus; 3 = 5, 3 on alamosa
Mis on potentsiaalne energia teaduse näites?

Potentsiaalne energia on talletatud energia, mis on objektil oma asukoha või oleku tõttu. Jalgratas mäe otsas, pea kohal hoitud raamat ja venitatud vedru omavad potentsiaalset energiat
