Sisukord:
Video: Kuidas leida teisendusmaatriksi?
2024 Autor: Miles Stephen | [email protected]. Viimati modifitseeritud: 2023-12-15 23:35
VIDEO
Lihtsalt, kuidas leida funktsiooni teisendus?
Funktsiooni tõlkimise/teisendusreeglid:
- f (x) + b nihutab funktsiooni b ühikuid ülespoole.
- f (x) – b nihutab funktsiooni b ühikuid allapoole.
- f (x + b) nihutab funktsiooni b ühikuid vasakule.
- f (x – b) nihutab funktsiooni b ühikuid paremale.
- –f (x) peegeldab funktsiooni x-teljel (st tagurpidi).
Võib ka küsida, mis teeb maatriksi lineaarseks? Kui ja millel on sama mõõde, on võimalik olla ümberpööratav, mis tähendab, et on olemas selline, et. See on alati nii.. Samuti a lineaarne teisendus vastendab read alati ridadeks (või nulliks). Peamine näide a lineaarne teisenduse annab maatriks korrutamine.
Samamoodi küsitakse, kuidas sa maatriksit loed?
Maatriks Märkus sisse maatriks A vasakule kirjutame a23 teise rea ja kolmanda veeru kirje tähistamiseks. Üks viis meeles pidada, et see tähistus seab read esikohale ja veerud teisele, on mõelda sellele sarnaselt lugemist raamat. Sina alati lugeda kõigepealt külili, nagu kirjutate alati esimesena read.
Mis teeb teisenduse lineaarseks?
A lineaarne teisendus on funktsioon ühest vektorruumist teise, mis austab aluseks olevat ( lineaarne ) iga vektorruumi struktuur. A lineaarne teisendus on tuntud ka kui a lineaarne operaator või kaart. Kahel vektoriruumil peab olema sama alusväli.
Soovitan:
Kuidas leida NaOH molekulmassi?
Vastus ja selgitus: naatriumhüdroksiidi molaarmass on 39,997 g/mol. Molaarmassi määramiseks korrutage aatommass valemis olevate aatomite arvuga
Kuidas leida kahe kiirusega keskmine kiirus?
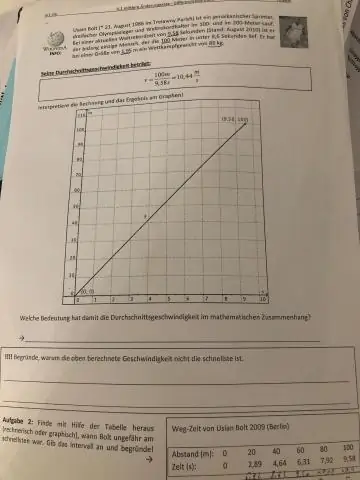
Keskmise leidmiseks jagatakse alg- ja lõppkiiruse summa 2-ga. Keskmise kiiruse kalkulaator kasutab valemit, mis näitab, et keskmine kiirus (v) võrdub lõppkiiruse (v) ja algkiiruse (u) summaga, jagatud 2-ga
Kuidas leida vedela segu erikaalu?
Nüüd jagage üldine tihedus vee tihedusega ja saate segu SG. Mis on suurima tihedusega vedelik? Kui segada kahte ainet võrdses mahus, on segu erikaal 4. Vedeliku mass tihedusega p segatakse võrdse massiga teise vedeliku tihedusega 3p
Kuidas leida logibaasi 2 10-st?
Log102 = 0,30103 (ligikaudne) Saate arvutada logaritme käsitsi, kasutades lihtsalt korrutamist (ja jagades astmetega 10 – mis on lihtsalt numbrite nihutamine) ja fakti, et log10(x10)=10⋅log10x, kuigi see pole kuigi praktiline
Kuidas leida isotoobi kaalutud keskmine?
18 neutroniga kloori isotoobi arvukus on 0,7577 ja massiarv 35 amu. Keskmise aatommassi arvutamiseks korrutage see osa iga isotoobi massinumbriga, seejärel lisage need kokku