Video: Kuidas leida parameetrilise võrrandi orientatsiooni?
2024 Autor: Miles Stephen | [email protected]. Viimati modifitseeritud: 2023-12-15 23:35
The suunas lennukist kõver kui parameeter suurenemist nimetatakse orientatsiooni selle kõver . The orientatsiooni lennukist kõver saab tähistada piki joonistatud nooltega kõver . Uurige allolevat graafikut. See on määratletud parameetrilised võrrandid x = cos(t), y = sin(t), 0≦t < 2Π.
Kuidas siinkohal teada saada graafiku orientatsiooni?
iga graafik on atsükliline orientatsiooni ; kõik atsüklilised orientatsioonid võib saada, asetades tipud jada ja suunates seejärel iga serva jada varasemast lõpp-punktist hilisemasse lõpp-punkti.
Lisaks, mis on parameetrite määramine? Matemaatikas ja täpsemalt geomeetrias parametriseerimine (või parameetrite määramine ; samuti parameetrite määramine , parametriseerimine) on protsess kõvera, pinna või üldisemalt kollektori või variatsiooni parameetriliste võrrandite leidmiseks, mis on määratletud kaudse võrrandiga.
Mis on siis parameetriline graaf?
Niisiis, a parameetriline kõver on määratletud kahe eraldi funktsiooni all kõvera -koordinaatide ja -koordinaatide jaoks kolmanda muutuja all, mida nimetatakse parameetriks. Sageli kasutatakse parameetrit "" ja seda kasutatakse sageli sümboolselt aja tähistamiseks, kui osake läbib kõverat.
Mis on vektorvõrrand?
Vektorvõrrand sirgjoonest Descartes võrrand sirge jaoks on y = mx + c, kus m tähistab sirge gradienti ja c on punkt, kus joon ristub y-teljega. A vektori võrrand joone jaoks vajab samamoodi 2 teavet: Punkt sirgel. Joone suund.
Soovitan:
Kuidas leida logaritmilise võrrandi asümptoot?
Põhipunktid Graafiliselt on logaritmiline funktsioon sarnane ruutjuure funktsiooniga, kuid vertikaalse asümptoodiga, kui x läheneb paremalt nullile. Punkt (1,0) on kõigi logaritmiliste funktsioonide graafikul kujul y=logbx y = l o g b x, kus b on positiivne reaalarv
Kuidas lahendate lineaarse ebavõrdsuse võrrandi?
Seal on kolm sammu: korraldage võrrand ümber nii, et "y" oleks vasakul ja kõik muu paremal. Joonistage joon y= (muutke see pidevaks jooneks y≤ või y≥ jaoks ja katkendjooneks y jaoks) Varjutage joone kohal, kui on suurem kui (y> või y≥) või joonest allapoole 'vähem kui' (y< või y≤)
Kuidas liigutada muutuja võrrandi teisele poole?
Reegel nr 2: suuruse või muutuja teisaldamiseks või tühistamiseks võrrandi ühel poolel tehke sellega "vastupidine" toiming võrrandi mõlemal poolel. Näiteks kui teil oli g-1=w ja soovite g isoleerida, lisage mõlemale poolele 1 (g-1+1 = w+1). Lihtsustage (sest (-1+1)=0) ja saage tulemuseks g = w+1
Kuidas leida algebraliselt võrrandi juuri?
Iga ruutvõrrandi juured on antud: x = [-b +/- sqrt(-b^2 - 4ac)]/2a. Kirjutage ruutarvud üles kujul ax^2 + bx + c = 0. Kui võrrand on kujul y = ax^2 + bx +c, asendage y lihtsalt 0-ga. Seda tehakse seetõttu, et võrrand on väärtused, kus y-telg on võrdne 0-ga
Kuidas lahendate võrrandi muutuja eraldamise teel?
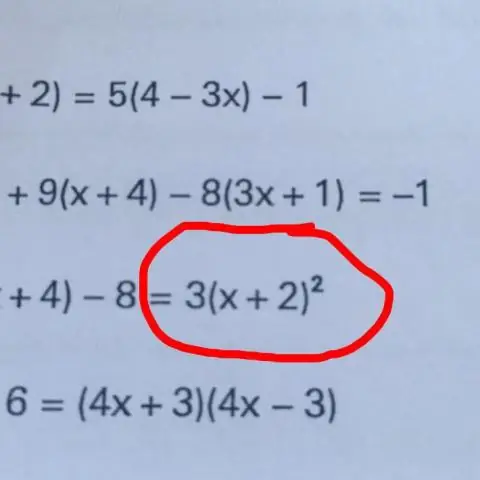
Põhimeetod muutuja eraldamiseks on võrrandi mõlema poole jaoks midagi teha, näiteks liita, lahutada, korrutada või jagada võrrandi mõlemad pooled sama arvuga. Seda protsessi korrates saame muutuja võrrandi ühel küljel isoleeritud