Sisukord:
Video: Kuidas tõestada, et maatriks on alamruum?
2024 Autor: Miles Stephen | [email protected]. Viimati modifitseeritud: 2023-12-15 23:35
Tsentraliseerija a Maatriks on alamruum Olgu V vektorruum n × n-st maatriksid , ja M∈V a fikseeritud maatriks . Defineeri W={A∈V∣AM=MA}. Siinset hulka W nimetatakse M tsentralisaatoriks V-s. Tõesta et W on a alamruum V.
Kuidas tõestada alamruumi?
Et näidata, et alamhulk on alamruum, peate näitama kolme asja:
- Näita, et see on lisamise all suletud.
- Näidake, et see on skalaarkorrutise korral suletud.
- Näidake, et vektor 0 on alamhulgas.
Lisaks, mis on maatriksi alus? Kui me otsime alus tuumast a maatriks , eemaldame tuumast kõik üleliigsed veeruvektorid ja säilitame lineaarselt sõltumatud veeruvektorid. Seetõttu a alus on lihtsalt kõigi lineaarselt sõltumatute vektorite kombinatsioon.
Tea ka, kas identiteedimaatriks on alamruum?
Eelkõige, identiteedi maatriks iseenesest (1 on põhidiagonaali all, 0 mujal) ei ole a alamruum kollektsioonist 2×2 maatriksid , sest kui identiteedi maatriks Olen selles alamruum , siis c ma pean olema selles alamruum kõikidele numbritele c.
Mis on maatriksi alamruum?
A alamruum on vektorruum, mis sisaldub teises vektorruumis. Nii et iga alamruum on vektorruum omaette, kuid see on määratletud ka mõne teise (suurema) vektorruumi suhtes.
Soovitan:
Kuidas on sõna maatriks seotud mitokondritega?
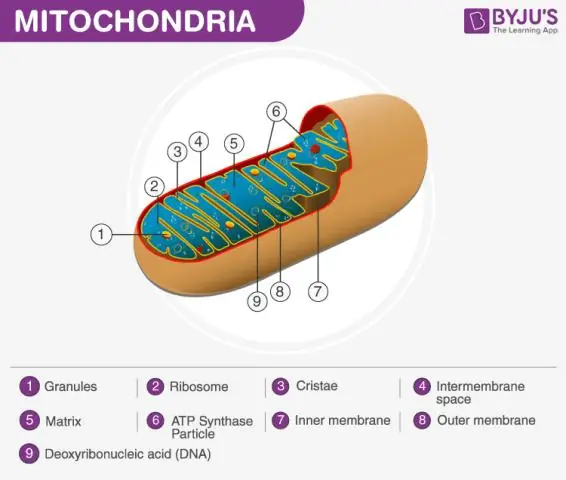
Määratletud mitokondriaalne maatriks Mitokondrid koosneb välismembraanist, sisemembraanist ja geelitaolisest materjalist, mida nimetatakse maatriksiks. See maatriks on viskoossem kui raku tsütoplasma, kuna see sisaldab vähem vett. See on rakuhingamise oluline samm, mis toodab energiamolekule, mida nimetatakse ATP-ks
Kas p2 on p3 alamruum?
Jah! Kuna iga polünoom astmega kuni 2 on ka polünoom astmega kuni 3, on P2 P3 alamhulk. Ja me juba teame, et P2 on vektorruum, seega on see P3 alamruum. See tähendab, et R2 ei ole R3 alamhulk
Kuidas tõestada, et sirged on tõestustes paralleelsed?
Esimene on see, kui vastavad nurgad, nurgad, mis on igal ristmikul samas nurgas, on võrdsed, siis on sirged paralleelsed. Teine on see, et kui alternatiivsed sisenurgad, nurgad, mis asuvad ristsirgete vastaskülgedel ja paralleelsete joonte sees, on võrdsed, on jooned paralleelsed
Kuidas tõestada, et miski on aluseks?
VIDEO Samuti küsiti, mis teeb aluse? Matemaatikas nimetatakse vektorruumis V olevate elementide (vektorite) hulka B a alus , kui V iga elementi saab kirjutada ainulaadsel viisil B elementide (lõpliku) lineaarse kombinatsioonina. alus kutsutakse alus vektorid.
Kuidas muuta maatriks identiteedimaatriksiks?
VIDEO Veelgi enam, kuidas leida identiteedimaatriksi abil maatriksi pöördväärtus? See toimib samamoodi maatriksid . Kui korrutada a maatriks (näiteks A) ja selle vastupidine (antud juhul A – 1 ), saate selle identiteedi maatriks I.